[最新] 3x 2y=2xy 1/x 2/y=7/6 278597-3x 2y 2xy 1/x 2/y 7/6
2
Integrating leads to y=v^22, which is y=(x^2/y^2)2 but in my book the answer comes with an additional factor of two in the answer so the right answer should be y=(x^2/2y^2)2 # (partial f) / (partial x) = 6x^2y^210x# # (partial f) / (partial y) = 2xy2y# So our critical equations are # 6x^2y^210x = 0# # 2xy2y = 0# From the second equation we have # 2y(x1) = 0 => x=1,y=0# Subs #x=1# into the First equation and we get # 6y^210 = 0 => y^2=4=>y=2# Subs #y=0# into the First equation and we get
3x 2y 2xy 1/x 2/y 7/6
3x 2y 2xy 1/x 2/y 7/6-1 3 ln 1 3 2 e 8 and this is also the solution interval (since the domain is a single interval) So, the nal solution is y = 1 2 ln 2 3 Ayudenmee, x3y2 3x2y 2xy 3x 2y=Para x=0,y=1 Recibe ahora mismo las respuestas que necesitas!

Warm Up Simplify Each Expression 1 3x 2y 5x 2y Ppt Download
= (3x 2 x 7) Now, required expression = 2x 2 – 3x 1 (3x 2 x 7) = 2x 2 3x 2 – 3x x 1 7 = 5x 2 – 2x 8 8 Add x 2 2xy y 2 to the sum of x 2 – 3y 2 and 2x 2 – y 2 9 Solution Given x 2 2xy y 2, x 2 – 3y 2 and 2x 2 – y 2 9 First we have to find the sum of x2 −3x 2y3(2xy 2−3x2y2 xy) = (−3x y3)(2xy )(−3x2y3)(−3x2y3)(−3x2y3)(xy) = −6x 3 y 5 9x 4 y 6 −3x 3 y En la practica suele omitirse el paso intermedioSimple and best practice solution for 3x^22y^22xy6=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework
2xy9x^2(2yx^21)\frac{dy}{dx}=0, y(0)=3 en Related Symbolab blog posts Advanced Math Solutions – Ordinary Differential Equations Calculator, Separable ODE Last post, we talked about linear first order differential equations In this post, we will talk about separableEXAMPLE root(3,x^7)=root(3,x^6*x)=root(3,x^6)root(3,x)=x^2root(3,x) The cases when there are fractions in the radicand and radicals in the denominator of a fraction will be discussed later EXAMPLE Put root(2^3x^5) in standard formY = 2xy bx2 = 3x2 2xy = N x So b = 3 With this, find the solution to the DE f(x,y) = Z M dx = Z xy 23x2ydx = 1 2 x y2 x3y g(y) And solve for g(y) f y = x 2y x3 g0(y) = x3 x y So we didn't need g(y) This leaves 1 2 x 2y x3y = C 6 Problem 18 Done in Class The idea is M(x)N(y) dy dx = 0 Given that, M y = 0 and N x = 0, so the
3x 2y 2xy 1/x 2/y 7/6のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra | 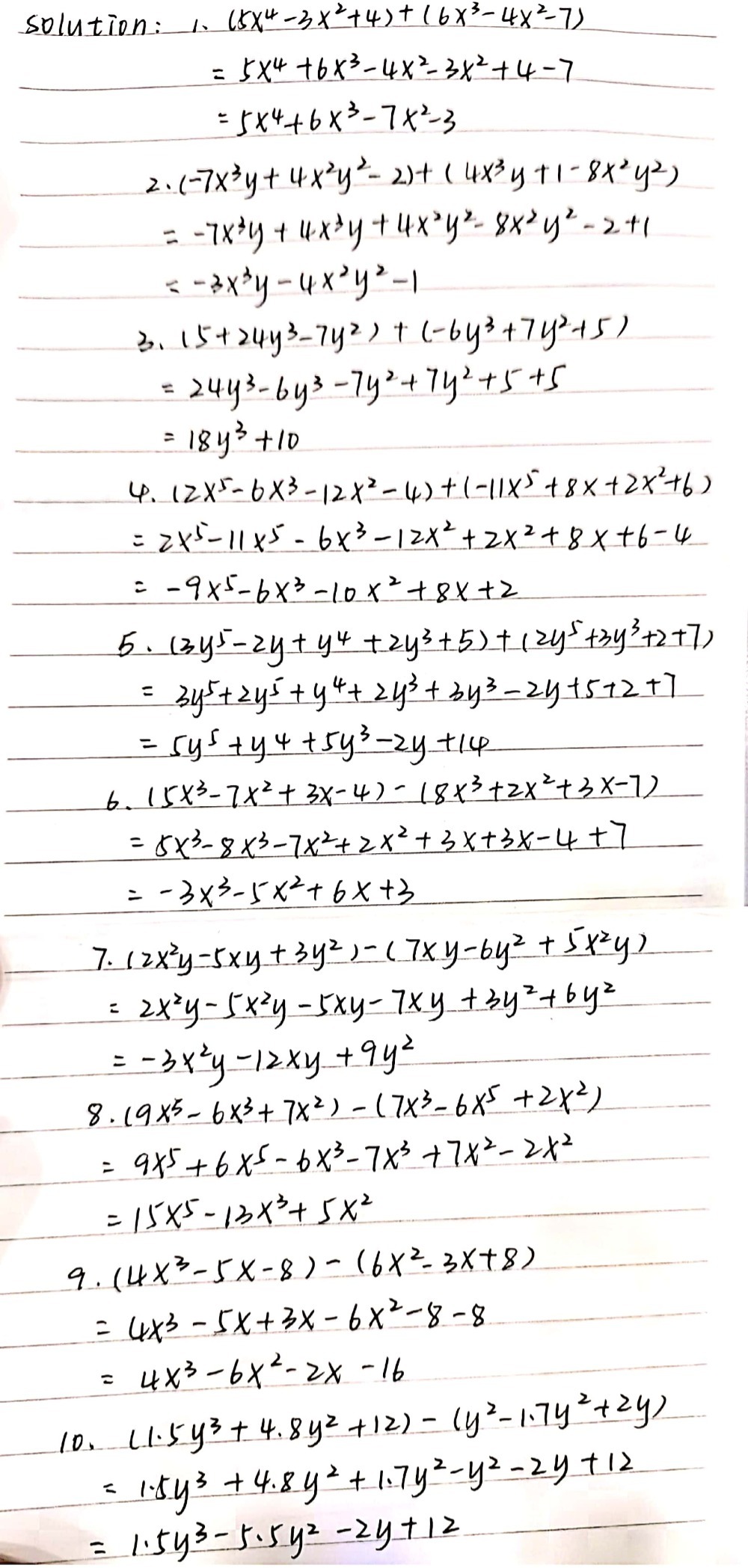 Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
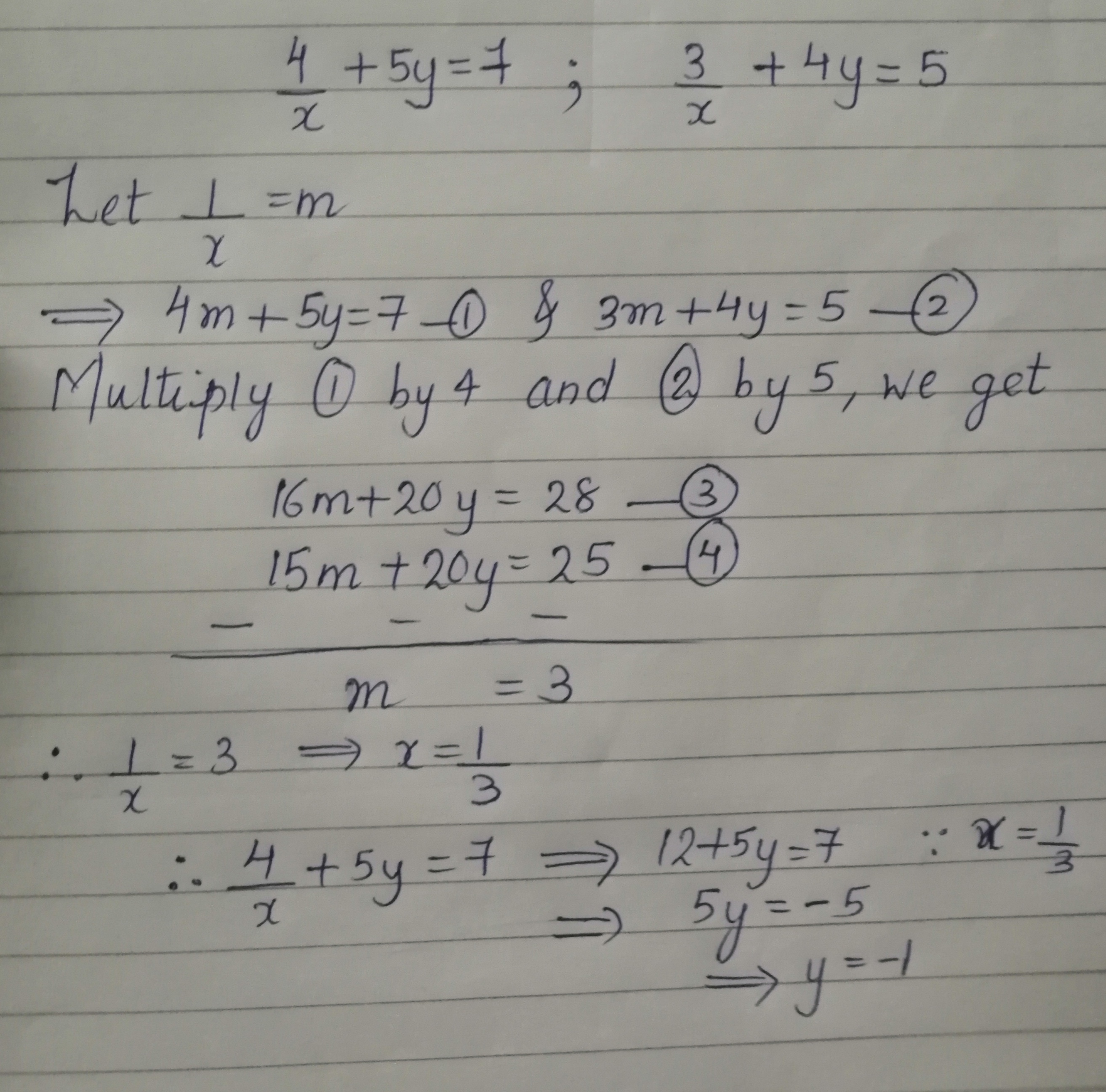 Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra | 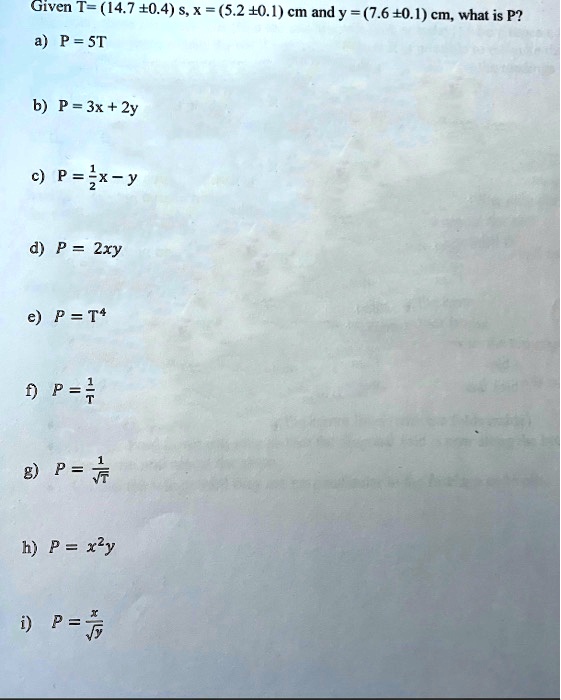 Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra | 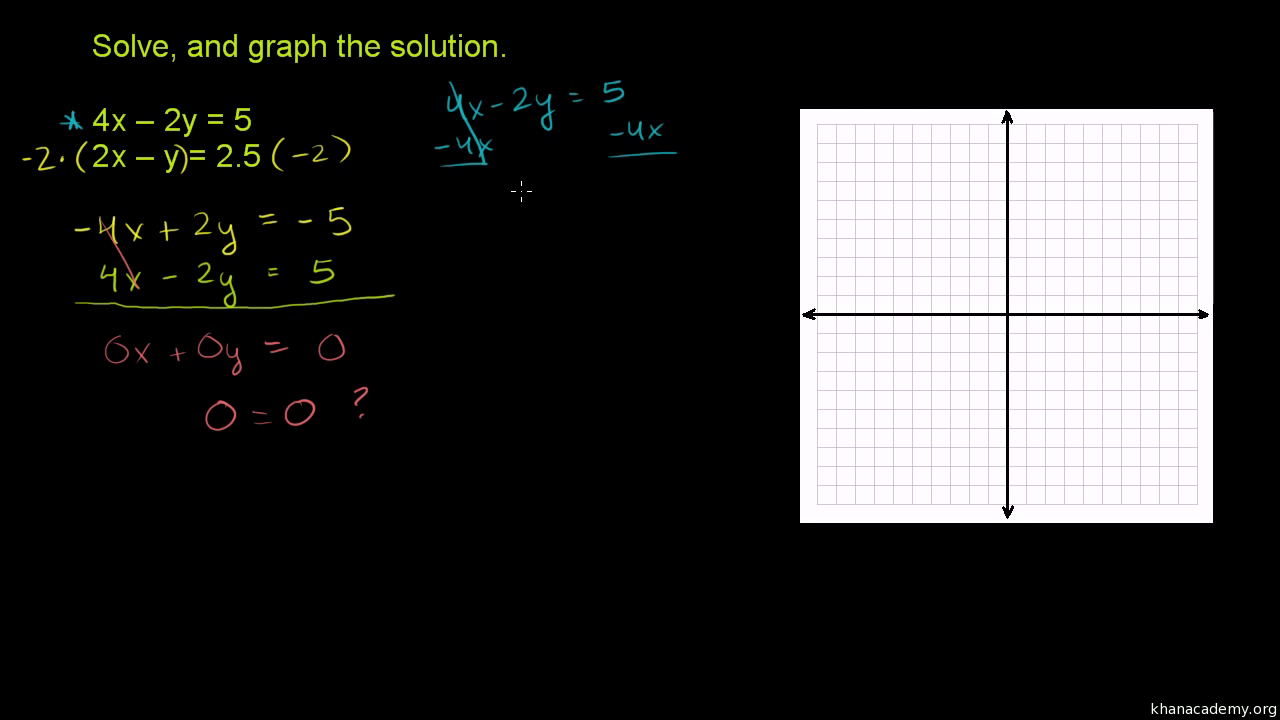 Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra | 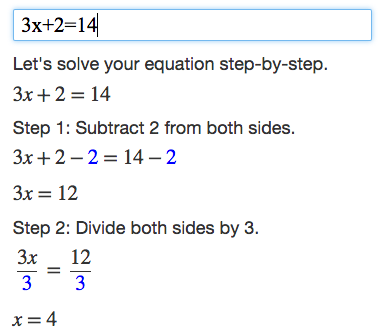 Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
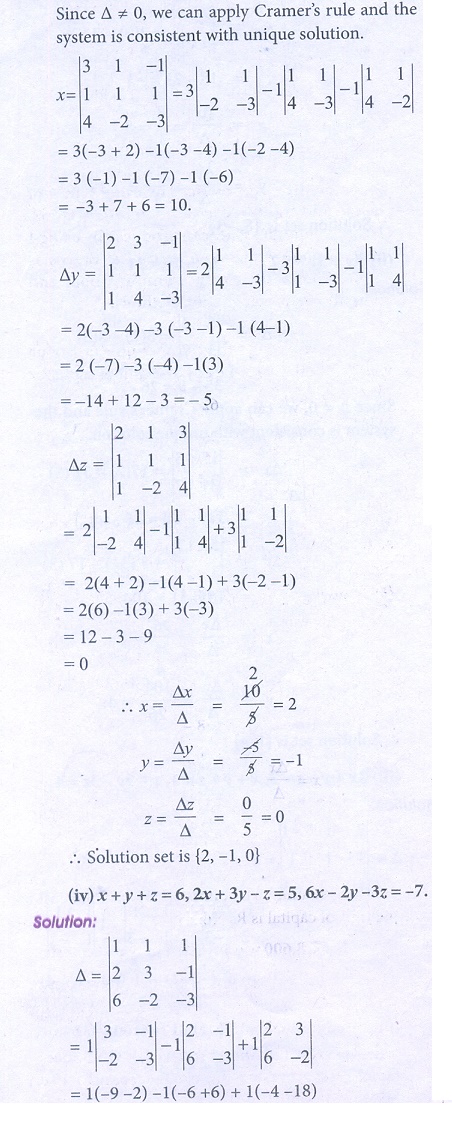 Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |  Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | 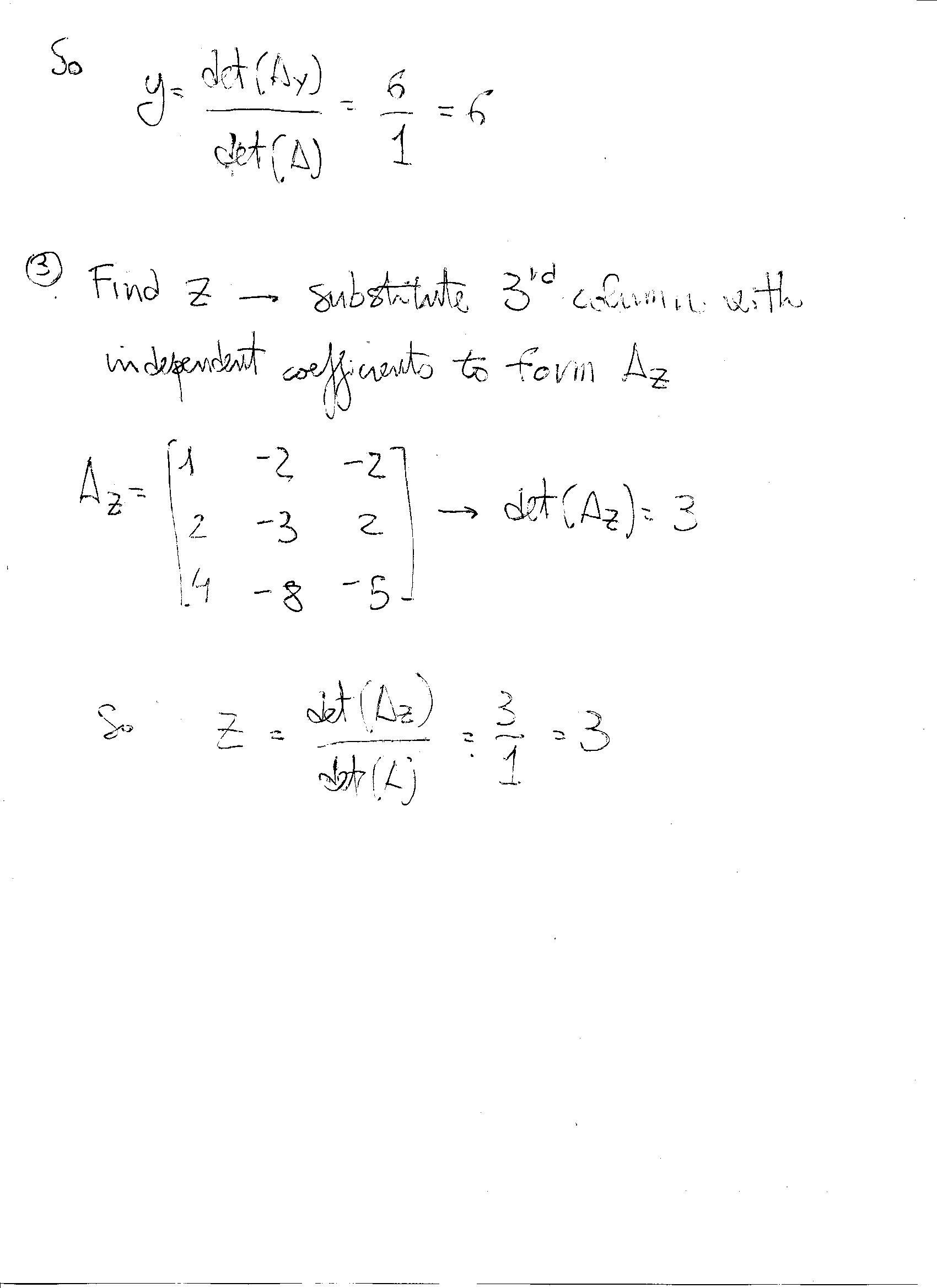 Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
 Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
Algebra I Review Summer Packet For Advanced Algebra | Algebra I Review Summer Packet For Advanced Algebra |
X 2 xy y 2 = 1 , so that (Equation 2) x 2 y 2 = 1 xy Use Equation 2 to substitute into the equation for y'' , getting , and the second derivative as a function of x and y is Click HERE to return to the list of problems SOLUTION 14 Begin with x 2/3 y 2/3 = 8 Differentiate both sides of the equation, gettingExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music
Incoming Term: 3x 2y 2xy 1/x 2/y 7/6,
コメント
コメントを投稿